Math 420/620
Fall 1999
Problem Set 4
Problems denoted (G) are only required of the graduate students.
- Given a group
 we recall that a commutator is an element of the form
we recall that a commutator is an element of the form  with
with 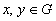 and that
and that  , the commutator subgroup, is a normal subgroup of
, the commutator subgroup, is a normal subgroup of 
- Show that the quotient group
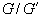 is abelian.
is abelian.
- (G)
Show that  is minimal with respect to this property. That is, if
is minimal with respect to this property. That is, if  is abelian, then
is abelian, then  (Hence
(Hence 
).
- Let
 be a homomorphism of groups. Show that ker(
be a homomorphism of groups. Show that ker( ) is a normal subgroup of
) is a normal subgroup of 
- Let
 be a group and
be a group and  a subgroup of
a subgroup of 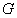
.
- Show that if
 , then
, then  is normal in
is normal in 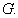
- Given an example of groups
 with
with  with
with 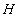 not normal in
not normal in 
- Let
 be a group with center
be a group with center 
.
- Show that
 is normal in
is normal in  .
.
- (G)
Show that  is cyclic
is cyclic 

is abelian.
- (G)
Show that every finitely generated subgroup of Q (the rational numbers) is cyclic, but that Q itself is not finitely generated.
- (G)
Let  and
and  be normal subgroups of
be normal subgroups of  with
with  . Show that
. Show that  for all pairs
for all pairs  and
and 
.
