Math 420/620

Fall 1999

Final Exam

 

  1. Let be a UFD, show that is irreducible if and only if it is prime.

    2.  

  2. Consider the ring Z. We define the norm map by
. Show the norm has the following properties:

 

  1. for all
  2. is a unit in

 

Use these facts to show that the ring Z is not a UFD.

 
  1. Show the following conditions are equivalent:
  1. is a PID
  2. is a UFD and every nonzero prime ideal of
is maximal.

 

  1. a) Construct an example of a ring that has precisely maximal ideals.

    2. b) (G) If your example from a) is not a domain, then make a new example which is a domain (reverse the instructions if your example from a) is a domain).

     

  2. Consider that the polynomial ring
. Show that the following conditions are equivalent.

 

  1. is a PID
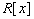  2. is a Euclidean domain
is a field.

 

  1. (G) Let be a domain with quotient field We say that is integral if is a root of a monic polynomial with coefficients in Show that if is a UFD and is integral, then

    2.  

  2. Let be commutative with identity. Let be any ideal and let . Show that is an ideal of and that