Estimating Distances Between Genes
Estimating Linkage From Three-Point Crosses
Deriving Linkage Distance and Gene Order From Three-Point Crosses
By adding a third gene, we now have several different types of crossing over products that can be obtained. The following figure shows the different recombinant products that are possible.
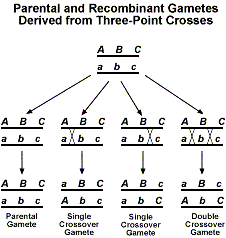
Now if we were to perform a testcross with F1, we would expect a 1:1:1:1:1:1:1:1 ratio. As with the two-point analyzes described above, deviation from this expected ratio indicates that linkage is occurring. The best way to become familiar with the analysis of three-point test cross data is to go through an example. We will use the arbitrary example of genes A, B, and C. We first make a cross between individuals that are AABBCC and aabbcc. Next the F1 is testcrossed to an individual that is aabbcc. We will use the following data to determine the gene order and linkage distances. As with the two-point data, we will consider the F1 gamete composition.
| Genotype | Observed | Type of Gamete |
|---|---|---|
| ABC |
390 |
Parental |
| abc |
374 |
Parental |
| AbC |
27 |
Single-crossover between genes C and B |
| aBc |
30 |
Single-crossover between genes C and B |
| ABc |
5 |
Double-crossover |
| abC |
8 |
Double-crossover |
| Abc |
81 |
Single-crossover between genes A and C |
| aBC |
85 |
Single-crossover between genes A and C |
| Total |
1000 |
The best way to solve these problems is to develop a systematic approach. First, determine which of the the genotypes are the parental gentoypes. The genotypes found most frequently are the parental genotypes. From the table it is clear that the ABC and abc genotypes were the parental genotypes.
Next we need to determine the order of the genes. Once we have determined the parental genotypes, we use that information along with the information obtained from the double-crossover. The double-crossover gametes are always in the lowest frequency. From the table the ABc and abC genotypes are in the lowest frequency. The next important point is that a double-crossover event moves the middle allele from one sister chromatid to the other. This effectively places the non-parental allele of the middle gene onto a chromosome with the parental alleles of the two flanking genes. We can see from the table that the C gene must be in the middle because the recessive c allele is now on the same chromosome as the A and B alleles, and the dominant C allele is on the same chromosome as the recessive a and b alleles.
Now that we know the gene order is ACB, we can go about determining the linkage distances between A and C, and C and B. The linkage distance is calculated by dividing the total number of recombinant gametes into the total number of gametes. This is the same approach we used with the two-point analyses that we performed earlier. What is different is that we must now also consider the double-crossover events. For these calculations we include those double-crossovers in the calculations of both interval distances.
So the distance between genes A and C is 17.9 cM [100*((81+85+5+8)/1000)], and the distance between C and B is 7.0 cM [100*((27+30+5+8)/1000)].
Now let's try a problem from Drosophila, by applying the principles we used in the above example. The following table gives the results we will analyze.
| Genotype | Observed | Type of Gamete |
|---|---|---|
| v cv+ ct+ |
580 |
Parental |
| v+ cv ct |
592 |
Parental |
| v cv ct+ |
45 |
Single-crossover between genes ct and cv |
| v+ cv+ ct |
40 |
Single-crossover between genes ct and cv |
| v cv ct |
89 |
Single-crossover between genes v and ct |
| v+ cv+ ct+ |
94 |
Single-crossover between genes v and ct |
| v cv+ ct |
3 |
Double-crossover |
| v+ cv ct+ |
5 |
Double-crossover |
| Total |
1448 |
Step 1: Determine the parental genotypes.
The most abundant genotypes are the partenal types. These genotypes are v cv+ ct+ and v+ cv ct. What is different from our first three-point cross is that one parent did not contain all of the dominant alleles and the other all of the recessive alleles.
Step 2: Determine the gene order
To determine the gene order, we need the parental genotypes as well as the double crossover geneotypes As we mentioned above, the least frequent genotypes are the double-crossover geneotypes. These geneotypes are v cv+ ct and v+ cv ct+. From this information we can determine the order by asking the question: In the double-crossover genotypes, which parental allele is not associated with the two parental alleles it was associated with in the original parental cross. From the first double crossover, v cv+ ct, the ct allele is associated with the v and cv+ alleles, two alleles it was not associated with in the original cross. Therefore, ct is in the middle, and the gene order is v ct cv.
Step 3: Determing the linkage distances.
-
v - ct distance caluculation. This distance is derived as follows: 100*((89+94+3+5)/1448) = 13.2 cM
-
ct - cv distance calculation. This distance is derived as follows: 100*((45+40+3+5)/1448) = 6.4 cM
Step 4. Draw the map.

Three-point crosses also allows one to measure interference (I) among crossover events within a given region of a chromosome. Specifically, the amount of double crossover gives an indication if interference occurs. The concept is that given specific recombination rates in two adjacent chromosomal intervals, the rate of double-crossovers in this region should be equal to the product of the single crossovers. In the v ct cv example described above, the recombination frequency was 0.132 between genes v and ct, and the recombination frequency between ct andcv was 0.064. Therefore, we would expect 0.84% [100*(0.132 x 0.64)] double recombinants. With a sample size of 1448, this would amount to 12 double recombinants. We actually only detected 8.
To measure interference, we first calculate the coefficient of coincidence (c.o.c.) which is the ratio of observed to expected double recombinants. Interference is then calculated as 1 - c.o.c. The formula is as follows:
![]()
For the v ct cvdata, the interference value is 33% [100*(8/12)].
Most often, interference values fall between 0 and 1. Values less than one indicate that interference is occurring in this region of the chromosome.
Copyright © 1998. Phillip McClean